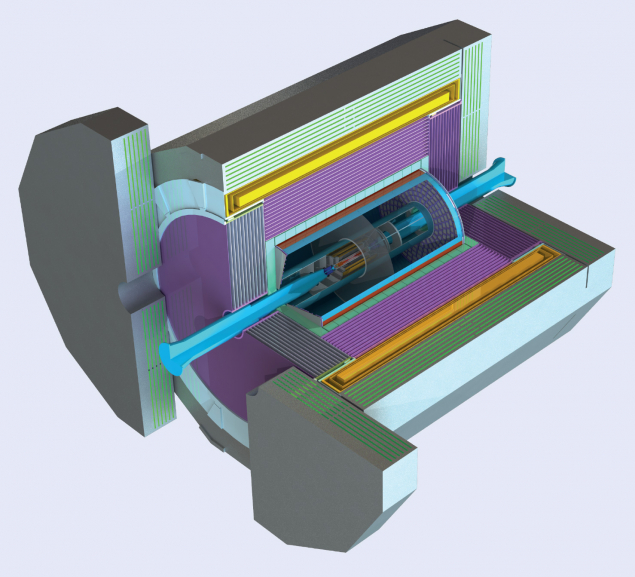
In October, the Circular Electron–Positron Collider (CEPC) study group completed its full suite of technical design reports, marking a key step for China’s Higgs-factory proposal. However, CEPC will not be considered for inclusion in China’s next five-year plan (2026–2030).
“Although our proposal that CEPC be included in the next five-year plan was not successful, IHEP will continue this effort, which an international collaboration has developed for the past 10 years,” says study leader Wang Yifang, of the Institute of High Energy Physics (IHEP) in Beijing. “We plan to submit CEPC for consideration again in 2030, unless FCC is officially approved before then, in which case we will seek to join FCC, and give up CEPC.”
Electroweak precision
CEPC has been under development at IHEP since shortly after the discovery of the Higgs boson at CERN in 2012. To enable precision studies of the new particle, Chinese physicists formally proposed a dedicated electron–positron collider in September 2012. Sharing a concept similar to the Future Circular Collider (FCC) proposed in parallel at CERN, CEPC’s high-luminosity collisions would greatly improve precision in measuring Higgs and electroweak processes.
“CEPC is designed as a multi-purpose particle factory,” explains Wang. “It would not only serve as an efficient Higgs factory but would also precisely study other fundamental particles, and its tunnel can be re-used for a future upgrade to a more powerful super proton–proton collider.”
Following completion of the Conceptual Design Report in 2018, which defined the physics case and baseline layout, the CEPC collaboration entered a detailed technical phase to validate key technologies and complete subsystem designs. The accelerator Technical Design Report (TDR) was released in 2023, followed in October 2025 by the reference detector TDR, providing a mature blueprint for both components.
Although our proposal that CEPC be included in the next five-year plan was not successful, IHEP will continue this effort
Wang Yifang
Compared to the 2018 detector concept, the new technical report proposes several innovations. An electromagnetic calorimeter based on orthogonally oriented crystal bars and a hadronic calorimeter based on high-granularity scintillating glass have been optimised for advanced particle-flow algorithms, improving their energy resolution by a factor of 10 and a factor of two, respectively. A tracking detector employing AC-coupled low-gain avalanche-diode technology will enable simultaneous 10 µm position and 50 ps time measurements, enhancing vertex and flavour tagging. Meanwhile, a readout chip developed in 55 nm technology will achieve state-of-the-art performance at 65% power consumption, enabling better resolution, large-scale integration and reduced cooling-pipe materials. Among other advances, a new type of high-density, high-yield scintillating glass forms the possibility for a full absorption hadronic calorimeter.
To ensure the scientific soundness and feasibility of the design, the CEPC Study Group established an International Detector Review Committee in 2024, chaired by Daniela Bortoletto of the University of Oxford.
Design consolidation
“After three rounds of in-depth review, the committee concluded in September 2025 that the Reference Detector TDR defines a coherent detector concept with a clearly articulated physics reach,” says Bortoletto. “The collaboration’s ambitious R&D programme and sustained technical excellence have been key to consolidating the major design choices and positioning the project to advance from conceptual design into integrated prototyping and system validation.”
CEPC’s technical advance comes amid intense international interest in participating in a Higgs factory. Alongside the circular FCC concept at CERN, Higgs factories with linear concepts have been proposed in Europe and Japan, and both Europe and the US have named constructing or participating in a Higgs factory as a strategic priority. Following China’s decision to defer CEPC, attention now turns to Europe, where the ongoing update of the European Strategy for Particle Physics will prioritise recommendations for the laboratory’s flagship collider beyond the HL-LHC. Domestically, China will consider other large science projects for the 2026 to 2030 period, including a proposed Super Tau–Charm Facility to succeed the Beijing Electron–Positron Collider II.
With completion of its core technical designs, CEPC now turns to engineering design.
“The newly released detector report is the first dedicated to a circular electron–positron Higgs factory,” says Wang. “It showcases the R&D capabilities of Chinese scientists and lays the foundation for turning this concept into reality.”
Further reading
CEPC Study Group 2025 arXiv:2510.05260.